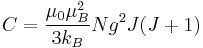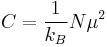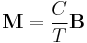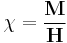Curie constant
The Curie constant is a material-dependent property that relates a material's magnetic susceptibility to its temperature.
The Curie constant, when expressed in SI units, is given by
where 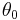 is the permeability constant,
is the permeability constant,  is the number of magnetic atoms (or molecules) per unit volume, (according to Cullity, N is the Avogadro's number;[2] Kittel does not talk about the meaning),
is the number of magnetic atoms (or molecules) per unit volume, (according to Cullity, N is the Avogadro's number;[2] Kittel does not talk about the meaning),  is the Landé g-factor,
is the Landé g-factor, 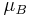 (9.27400915e-24 J/T or A·m2) is the Bohr magneton,
(9.27400915e-24 J/T or A·m2) is the Bohr magneton, 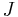 is the angular momentum quantum number and
is the angular momentum quantum number and 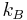 is Boltzmann's constant. For a two-level system with magnetic moment
is Boltzmann's constant. For a two-level system with magnetic moment  , the formula reduces to
, the formula reduces to
The constant is used in Curie's Law, which states that for a fixed value of a magnetic field, the magnetization of a material is (approximately) inversely proportional to temperature.
This equation was first derived by Pierre Curie.
Because of the relationship between magnetic susceptibility 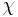 , magnetization
, magnetization 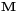 and applied magnetic field
and applied magnetic field 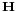 :
:
this shows that for a paramagnetic system of non-interacting magnetic moments, magnetization 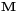 is inversely related to temperature
is inversely related to temperature  (see Curie's Law).
(see Curie's Law).